�@�ł͑��s���܂��B�@�@�@�@�@�@�@�@�@
�@����ɍׂ����\������Ȃ�O,�T�f�V�x���Ƃ����l���g���܂��B
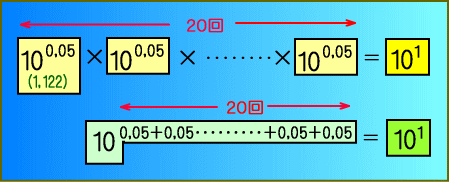
�@�O,�T�f�V�x���@�́@�O,�O�T�x�����P�^�Q�O�x���@�܂��@�P�O�̂Q�O�捪�@�ŁA���ׂĂ݂��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�u�P,�P�Q�Q�v�@�ƂȂ�A
�@���̐��l���Q�O�����킹��Ɩ�P�O�ƂȂ�܂��B
�@������p�l���ɂ��܂����B�������ĕ�����ɂ����ł��傤���H
�@
�@�\�����܂����B
| �f�V�x�� | �W��B | �O,�T��B |
| ��@�� | �P�O�O,�W | �P�O�O,�O�T |
| �{�@�� | �U,�R�P�R | �P,�P�Q�Q |
�@��̕\�ɂ���@�W���a�@�́@�U,�R�P�R�{�@�Ɂ@�O,�T���a�@�́@�P,�P�Q�Q�{�@��d��Ŋ|���Z�����
�@�@�@�@�@�V,�O�W�R�{�@�ɂȂ�܂��B�����Ł@�@�@
|
|
�@�܂��@�V�@�Ƃ��������́A�قځ@�P�O�̂O,�W�T��@�ł�����킯�ł��B
�@�܂��A�O,�T���a�@�́@��P,�P�{�@��\���A�����ƃx�����Ȓl�ł��B
�@����ł��P�O�p�[�Z���g�ɂȂ�����A�u����ł̓v���X�O,�T�f�V�x��������B�v
�@�ȂǂƒN�����Ԃ₭���ł��傤����B
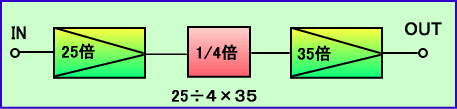
�@����͂Ƃ������A�Q�T�{�@�̑�����ƁA�R�T�{�@�̑����킪����A
�@���̒��ԂɁ@�P�^�S�{�@�Ɍ��������H���͂��܂��Ă���ꍇ�A
�@�g�[�^���ʼn��{�ɂȂ�̂��ɂ��Čv�Z���Ă݂܂��傤�B
�@�@�@�@�@�@ �@�@�@�@
�@�@�@�@
�@�������A
|
�@�@�@�@�@�|�U���a���|�O,�U�a���P�O�|�O,�U |
�@�Q�T�{�@�́@�T�~�T�{�@�ŁA������f�V�x���Ō���Ɓ@�V���a�{�V���a���P�S���a
�@�R�T�{�@�́@�T�~�V�{�@�ŁA������f�V�x���Ō���Ɓ@�V���a�{�W,�T���a���P�T,�T���a
�@�S���̂P�@�́@�S�{�@�ł���@�U���a�@�̋t���@�܂�@�[�U���a�B
���̗l�q���p�l���ɂ��܂����B
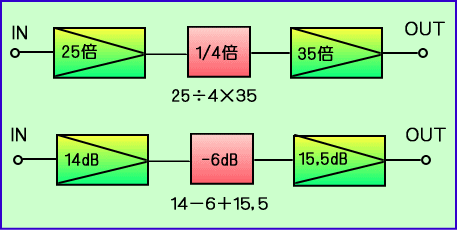
�@�����{���܂�|���Z�Ōv�Z����ƁA������Ɩ��ł����A
�@���a�\���ł͏搔�̌v�Z�A�܂葫���Z�ƈ����Z�ɂȂ�̂�
�@�@�@�@�P�S�|�U�{�P�T�C�T���Q�R�C�T�@�ƈÎZ�ł��o���Ă��܂��܂��B
�@�����ďo�Ă����@�Q�R�C�T���a�@���A���x�͕������Ă���f�V�x���ɕ������܂��B����Ɓ@
|
���P�O�O�{�~�Q�{�~�P�C�P�{ |
�@�ƁA�����悻�̔{�����ȒP�ɂ����܂����A�����ƕ��G�ȉ�H�ł͂���ɗ͂����܂��B
�@�u�ł��A����Ȃ̓d��Ŕ{�������v�Z����Ⴂ�������I�v�Ƃ����l�A
�@�����d��Ōv�Z���Ă��������B
�@�@�@�@�@�Q�T���S�~�R�T���Q�P�W�C�V�T�{
�@�����A���̎�@���������ꂽ�̂́A�d��͂��납�J�V�I�v�Z�@�Ƃ�����Ђ��A���₻��ǂ��납�A
�@���̑n�ݎ҂ł���~���В��i�P�X�Q�X�`�j���琶�܂�Ă��Ȃ��A��������吳���ゾ�Ƃ��������A�Y��Ȃ��ł��������B
|
�A�����Ŋ|���Z�⊄��Z���A�搔�̑����Z������Z�ɒu�������邱�ƂŁA�P�������Ă��܂����Ƃ����A��@�Ȃ̂ł��B |
�@���Ƃ͂��a�Ɣ{���̊W���o���邾���ł����A����́u����v��������܂���B
�@���̕\�̓v���X�����������Ă���܂��A�f�V�x���Ƀ}�C�i�X�L��������
�@�u���{�v�Ƃ����������u�����̂P�v�ƕς�邾���ł��B
| ���̉� | �O�� | �P�� | �Q�� | �R�� | �S�� | �T�� | �U�� | �V�� | �W�� | �X�� |
| �f�V�x�� | �P��B | �Q��B | �R��B | �S��B | �T��B | �U��B | �V��B | �W���� | �X���� | �P�O���� |
| ��@�� | �P�O�O,�P | �P�O�O,�Q | �P�O�O,�R | �P�O�O,�S | �P�O�O,�T | �P�O�O,�U | �P�O�O,�V | �P�O�O,�W | �P�O�O,�X | �P�O�P,�O |
| �{�@�� | �P,�Q�T�X | �P,�T�W�T | �P,�X�X�U | �Q,�T�P�Q | �R,�P�U�R | �R,�X�W�Q | �T,�O�P�S | �U,�R�P�R | �V,�X�S�W | �P�O,�O�O�U |
| �T�@�� | �� | �P,�U�{ | �Q�{ | �Q,�T�{ | �R�{�� | �S�{ | �T�{ | �U,�R�{ | �W�{ | �P�O�{ |
�@�ƁA�����܂ŗ��Ċ̐S�Ȃ��Ƃ�Y��Ă��܂����B�O�f�V�x���͂P�{�ł����A�O�{�͂ǂ��\���̂ł��傤���B
�@����͂��̕����������Ă���܂��B
�@�@�@�@�@�@�P�^�����偁�O�@�@������u�P�O�̉��悩�H�v�ŕ\����
�@�@�@�@�@�@�@�P�^�P�O�����P�O�\��
�@�����Ń}�C�i�X������x�����}�C�i�X������f�V�x�����O�{�ɂȂ�킯�ł��B
| �f�V�x�� | �O��B | �|������ |
| �{�@�� | �P | �O |
�@����̃��|�[�g�ŁA�f�V�x���̊T�O�����߂Ē������ł��傤���B
| �@ �NjL�j�O�C�T�f�V�x�����O�C�O�T�x���̎Z�o���@�ɂ͂��̂悤�ȕ��@������܂��B ���̎������Ă������� �P���a���P�O�O�C�P���P�O�O�A�O�T�{�O�C�O�T �@���P�O�O�C�O�T�~�P�O�O�C�O�T �܂�P�f�V�x���Ƃ��O,�T�f�V�x���̂Q���ɂȂ�̂ŁA�t�ɂP�C�Q�T�X�̃��[�g���o���Όv�Z�ł��܂��B ���[�g�t���̓d��Łu�P�C�Q�T�X�v�Ƒł����݁A��L���������u�P�C�P�Q�Q�O�T�v�Əo��ł��傤�B�O�C�T�f�V�x���́A��P���A�b�v�������x�����Ȓl�ł��B |
| �f�V�x�� | �O,�T��B |
| �{�@�� | �P,�P�Q�Q |
| �T�@�� | �P,�P�{ |
�@�@�@�@�����@���i�M�_�@�J�c�~
�@�����܂łŁA�f�V�x���̊T�O�I�Ȃ��b�͏I���ł����A���͂���܂ŏq�ׂĂ����̂́A�S�ēd�͂̔{���Ȃ̂ł��B
�@���̐�͓d���̔{���ɂ��Ă̘b�ɂȂ�̂ŁA�����̂���l�͂��ǂ݂��������B
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�Ⴆ�P�O�I�[���̒�R��ɂP�O�{���g�̓d����������ƁA
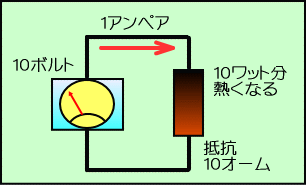
�@�P�O�{���g���P�O�I�[�����P�A���y�A�@�̓d��������܂��B���̎��̓d�͂�
�@�P�O�{���g�~�P�A���y�A���P�O���b�g�@�������d�����Q�{�ɂȂ��
�@�Q�O�{���g���P�O�I�[�����Q�A���y�A�@�̓d��������A���̎��̓d�͂�
�@�Q�O�{���g�~�Q�A���y�A���S�O���b�g�@���̂悤�ɂS�{�ɂȂ��Ă��܂��B
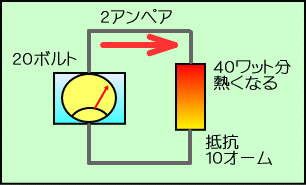
�@�S�{�Ƃ͂U�f�V�x���B�d�͂ł́A�m���Q�{�͂R�f�V�x���ł����B
�@���̂悤�ɁA�d���𐔔{�ɂ����Ɠd���܂œ����{�ɂȂ邽�߁A�d���̔{�����f�V�x���ŕ\�����鎞�́A
�@�Ⴆ�Γd�����Q�{�Ȃ�d�͂͂S�{�A�d�����R�{�Ȃ�d�͂͂X�{�Ƃ����悤�ɁA�@���ʓI�ɋN����d�͂̔{���@�ŕ\�����܂��B
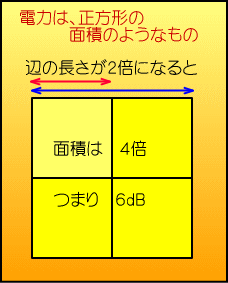
�@�����œd���̃f�V�x���\���ł́A�d�͂̃f�V�x���\�����Q�{�ɂ��܂��B
�@�Ⴆ�A�f�V�x���œd�͂́@�S�{�@������킷�Ɓ@�U�f�V�x�����P�O�O�C�U�ł���
�@�d�����S�{�ɂȂ�Ɠd�����@�S�{�@�ɂȂ�̂ŁA���ʓI�ɂ́@�P�U�{�@���Ӗ����܂��B
�@�����ōŏ������@���ʓI�ɋN����d�͂̔{���@�@�܂�@�P�U�{�@�ł���@�P�Q��B�@��
�@�d���ɂ�����@�S�{�@�Ƃ��邱�Ƃɂ��Ă����悢�̂ł��B
| �@�P�O�O,�U�~�P�O�O,�U���P�O�O,�U�{�O,�U �@�@�@���P�O�P,�Q �@�@�@���P�Q���a |
�@���̂悤���@���ʓI�ɋN����d�͂̔{���@�Ŏ����Ȃ�@�u�d���\���ł́A�d�͂̎����Q�{�f�V�x���v�ɂ��Ȃ���Ȃ�Ȃ��̂ł��B
|
�d�����P�O�{�ɂȂ������炾�ȁB �@�@�d�͂��U�f�V�x���i���S�{�j�オ�����̂́A �d�����Q�{�ɂȂ������炾�ȁB |
�@�Ɨ\�����邱�Ƃ��K�v�Ȃ킯�ł��B
�@�i�d���̔{���@�@�f�V�x���\�j
| �f�V�x�� | �P��B | �Q��B | �R��B | �S��B | �T��B | �U��B | �V��B | �W��B | �X��B | �P�O��B | �P�Q���� | �P�S��B | �P�U��B | �P�W��B | �Q�O��B |
| �{�@�� | �P,�P�Q�Q | �P,�Q�T�X | �P,�S�P�Q | �P,�T�W�T | �P,�X�O�O | �P,�X�X�O | �Q,�Q�R�X | �Q,�T�P�R | �Q,�W�P�X | �R,�P�U�R | �R,�X�W�Q | �T,�O�P�S | �U,�R�P�R | �V,�X�S�W | �P�O,�O�O�U |
| �T�@�� | �P,�P�{ | �P,�Q�U�{ | �P,�S�{ | �P,�U�{ | �P,�X�{ | �Q�{ | �Q,�Q�S�{ | �Q,�T�{ | �Q,�W�{ | �R,�Q�{ | �S�{ | �T�{ | �U,�R�{ | �W�{ | �P�O�{ |
�@��������قǂ̓d�͂̌v�Z���ł́A��R�����̒l�A�܂�P�O�I�[���Ƃ��Ă��܂����B
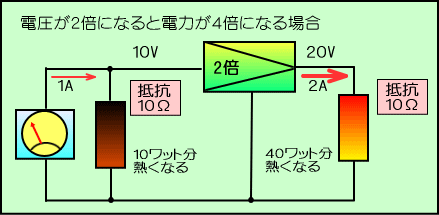
�@�Ƃ��낪�ŋ߂̉�H�ł́A���̒l�����Ȃ̂ŁA�d�����Q�{�ɂȂ����Ƃ��Ă��A�d�͂��S�{�ɂȂ��Ă���Ƃ͌���܂���B
�@���̐}�͂Q�{�ɂȂ�����̒�R�l���S�O���ɂȂ����ꍇ�ŁA�d�����Q�{�ł��d�����Q���̂P�ɂȂ������߁A
�@���Ǔd�͕͂ς���Ă��܂���B
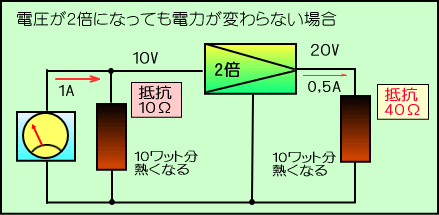
�@�����Łu���ʂƂ��ċN����d�͂̔{���v�Ƃ��������͖ڂ��ނ�A�P�Ȃ�{�����\���\�L���Ƃ��āA
�@���ׂēd�͂̎��̂Q�{�f�V�x���ōl����悤�ɂȂ��Ă��܂��B
�@�ł�����d���ł́@�P�f�V�x���@���@��P���A�b�v�@���Ӗ����܂��B
�@�O�̂��߁A������x�i�d���̔{���@�@�f�V�x���\�j�����ɋL�ڂ��Ă����܂��B
| �f�V�x�� | �P��B | �Q��B | �R��B | �S��B | �T��B | �U��B | �V��B | �W��B | �X��B | �P�O��B | �P�Q���� | �P�S��B | �P�U��B | �P�W��B | �Q�O��B |
| �{�@�� | �P,�P�Q�Q | �P,�Q�T�X | �P,�S�P�Q | �P,�T�W�T | �P,�X�O�O | �P,�X�X�O | �Q,�Q�R�X | �Q,�T�P�R | �Q,�W�P�X | �R,�P�U�R | �R,�X�W�Q | �T,�O�P�S | �U,�R�P�R | �V,�X�S�W | �P�O,�O�O�U |
| �T�@�� | �P,�P�{ | �P,�Q�U�{ | �P,�S�{ | �P,�U�{ | �P,�X�{ | �Q�{ | �Q,�Q�S�{ | �Q,�T�{ | �Q,�W�{ | �R,�Q�{ | �S�{ | �T�{ | �U,�R�{ | �W�{ | �P�O�{ |
�@�Ō�Ƀf�V�x���\���̌��p�ɂ��čl���Č��܂��傤�B
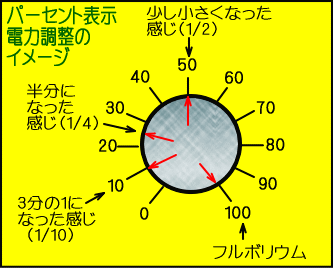
�@�Ⴆ�P�O�O�܂ŋϓ��ɖڐ��肪����A�c�}�~�̈ʒu�����̂܂܃A���v�̏o�͂��Ƃ���ƁA
�@�P�O�O�̏o�͂��ɂ��邽�߂ɂ́A�c�}�~���T�O�ɍ��킷���ƂɂȂ�܂��B
�@�Ƃ��낪�o�͂������ɂȂ��Ă��A���Œ����������ł́u������Ɖ��ʂ����������ȁB�v�Ƃ������x�ł�������܂���B
�@�������A���ꂪ�l�Ԃ̎��̓����Ȃ̂ł��B
 �@
�@
�@����ɔ����̂Q�T�ɂ��Ă��A�u�܂��A�ꉞ�͏������Ȃ����ȁB�v�Ƃ������x�ł����A
�@���ł������܂łŖڐ���̊p�x�̑唼���g���Ă��܂��B
�@����ł͐Â��ɉ��y���������A�c��킸���Ȋp�x�̒����ŁA���ʂ��傫���ς��Ƃ����A
�@�ƂĂ��g���Â炢�{���E���ɂȂ��Ă��܂��܂��B
�@���̂悤�ȃ{���E���́A�ʏ�B�J�[�u�̃{���E���Ƃ����܂��B
�@�ω����O���t�ɂ���ƒ����ɂȂ�̂Œ����^�{���E���Ƃ������܂��B
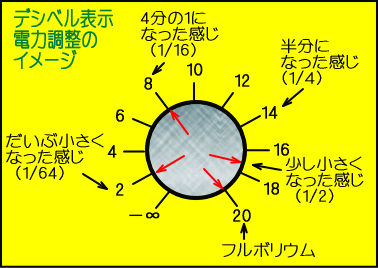
�@����f�V�x���ŋϓ��ɖڐ����Ă���ƁA�P�O�O�{�ł���Q�O�f�V�x���̔����Ƃ��}�C�i�X�R�f�V�x���ŁA
�@�c�}�~�̈ʒu�́A�P�V�̂�����ł��B
�@���̎��́u�c�}�~��������Ɖ������B�v�Ƃ������o�Ɓu���ʂ�������Ɖ��������B�v�Ƃ������o�͂ƂĂ��߂��̂ł��B
 �@
�@
�@����Ƀc�}�~���܂�P�O�f�V�x���̈ʒu�܂ʼn�����ƁA�o�͂͂P�O���̂P�ɂȂ�܂�
�@���A���̊��o�ł́u���ʂ������ɂȂ����B�v�Ƃ������o�ɋ߂��̂ł��B
�@���̂悤�ȃ{���E���́A�ʏ�A�J�[�u�̃{���E���Ƃ����܂��B
�@�ω��̃O���t�͑ΐ��J�[�u��`���̂őΐ��^�{���E���Ƃ������܂��B
�@�������C���X�g�̃{���E���͕�����₷�����邽�߁A���I�ȓd�͒����p�̃{���E���Ƃ��܂������A
�@��������̃{���E���͓d���������s�Ȃ��܂��B
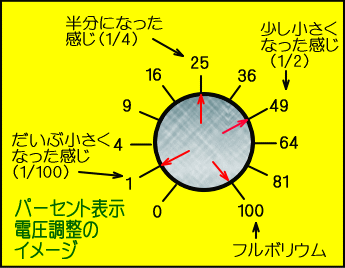
�@�����ŁA���ʂƂ��ċN����d�͂̕ω��͂Q��{�ƂȂ邽�߁A�����������o���قȂ�܂��B
�@�܂����ۂ̃c�}�~�̕\���́A��E�̃C���X�g�Ɠ����ł��B
 �@�@
�@�@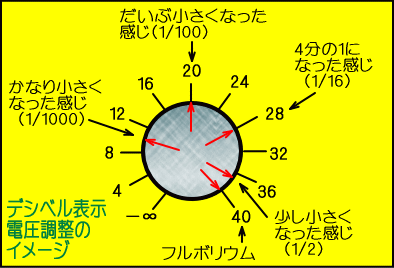
�@���̂悤�Ƀf�V�x���\���Ƃ����̂́A���l�ԓI�ȑ召���o�ɋ߂��̂ŁA
�@�����ł�����Ɏg�p����Ă���킯�ł��B